Sebuah fungsi f adalah suatu aturan korespondensi yang menghubungkan setiap objek x dalam satu himpunan, yang disebut daerah asal, dengan sebuah nilai tunggal f(x) dari suatu himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah hasil fungsi. Lihat gambar berikut :

Cara mencari daerah asal dan daerah hasil
Contoh : Carilah daerah asal dan daerah hasil dari fungsi

 

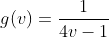Penyelesaian :
Daerah Asal untuk f adalah :

Daerah hasil adalah :
Rubah dulu fungsi diatas dengan variabel y menjadi

Membedakan fungsi satu-satu (one to one) dan Fungsi pada (onto)

Dalam suatu fungsi ada yang merupakan hanyaFungsi Pada atau Fungsi Satu-Satu saja tapi ada yang termasu kedua-duanya. Fungsi yang merupakan fungsi satu-satu dan pada biasanya disebut dengan Fungsi Bijeksi. 

Satu-Satu dan Fungsi Pada.

Secara sederhana bahwa Fungsi Bijeksi akan terjadi jika jumlah anggota domain sama dengan jumlah anggota kodomain. Dengan catatan bahwa tidak ada dua domain berbeda atau lebih dipetakan ke kodomain yang sama dan setiap kodomain memiliki pasangan di domain.

Keterangan :

Pemetaan pertama merupakan Fungsi Bijeksi karena sudah sesuai dengan Difinisi.

Pemetaan kedua bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi Pada. Perhatikan “d” dan “e” di domain, kedua anggota domain tersebut dipetakan ke anggota domain yang sama

Pemetaan ketiga bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi Satu-Satu. Karena terdapat anggota kodomain yaitu “9″ yang tidak memiliki pasangan pada anggota domain.

FUNGSI SATU KE SATU (ONE TO ONE)

Fungsi di atas, fungsi dikatakan satu-ke-satu (one-to-one) atau injektif (injective) jika tidak ada dua elemen himpunan A yang memiliki bayangan sama.

Contoh. Relasi adalah fungsi satu-ke-satu,
Tetapi relasi ke bukan fungsi satu-ke-satu,

FUNGSI PADA atau (ONTO)

Fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan B merupakan bayangan dari satu atau lebih elemen himpunan A.

Dengan kata lain seluruh elemen B merupakan jelajah dari f. Fungsi f disebut fungsi pada himpunan B. 

Membedakan domain, kodomain dan range suatu fungsi

Pengertian Domain, Kodomain, Range Domain disebut juga dengan daerah asal,

 kodomain daerah kawan, sedangkan range adalah daerah hasil.

contoh : Diketahui himpunan P = { 1,2,3,4 } dan himpunan Q = { 2,4,6,8,10,12 }

Relasi dari himpunan P ke himpunan Q dinyatakan dengan " setengah dari ".

Jika relasi tersebut dinyatakan dengan himpunan pasangan berurutan menjadi :

{ (1,2),(2,4),(3,6),(4,8) }.

Relasi di atas merupakan suatu fungsi karena setiap anggota himpunan P mempunyai tepat satu kawan anggota himpunan Q.

Dari fungsi di atas maka :

Domain/daerah asal = himpunan P = { 1,2,3,4 }

Kodomain/daerah kawan = himpunan Q = { 2,4,6,8,10,12 }

Range/daerah hasil = { 2,4,6,8 }

Jika A = {2, 3, 6} B = {2, 4, 6, 8, 10, 11}. Relasi dari himpunan A ke B adalah “

Faktor dari “, nyatakanlah relasi tersebut dengan :

a. Diagram Panah

b. Diagram Cartesius

c. Himpunan pasangan berurutan.

sehingga diperoleh daerah hasilnya adalah :