Konsep dan Notasi Dasar

Kalimat deklaratif yang bernilai benar (true) atau salah (false), tetapi tidak keduanya.

Semua pernyataan di bawah ini adalah proposisi:

1

a) 13 adalah bilangan ganjil.

b) 1 + 1 = 2.

c) 8  akar kuadrat dari 8 + 8.

d)  Untuk sembarang bilangan bulat n  0, maka 2n adalah bilangan genap.

e) Hari ini adalah hari Rabu.

 2

Semua pernyataan di bawah ini bukan proposisi

(a) Jam berapa kereta api Argo Bromo tiba di Gambir?

(b) Isilah gelas tersebut dengan air!

(c) x + 3 = 8

(d) x > 3

Proposisi dilambangkan dengan huruf kecil p, q, r, ….

p : 13 adalah bilangan ganjil.

q : Untuk sembarang bilangan bulat n  0, maka 2n adalah bilangan genap.

r : 2 + 2 = 4 2

Misalkan p dan q adalah proposisi.

1. Konjungsi (conjunction): p dan q

Notasi p  q,

2. Disjungsi (disjunction): p atau q

Notasi: p  q

3. Ingkaran (negation) dari p: tidak p

Notasi: p

p q p  q p q p  q p q

T T T T T T T F

T F F T F T F T

F T F F T T

F F F F F F

Contoh 3

Diketahui proposisi-proposisi berikut:

p : Pemuda itu tinggi

q : Pemuda itu tampan

Nyatakan dalam bentuk simbolik:

(a) Pemuda itu tinggi dan tampan

(b) Pemuda itu tinggi tapi tidak tampan

(c) Pemuda itu tidak tinggi maupun tampan

(d) Tidak benar bahwa pemuda itu pendek atau tidak tampan

(e) Pemuda itu tinggi, atau pendek dan tampan

(f) Tidak benar bahwa pemuda itu pendek maupun tampan

Penyelesaian:

(a) p  q

(b) p  q

(c) p  q

(d) (p  q)

(e) p  (p  q)

(f) (p  q)

Misalkan p dan q adalah proposisi.

1. Kondisional atau implikasi : p  q

2. Konvers (kebalikan) : q  p

3. Invers : ~ p  ~ q

4. Kontraposisi : ~ q  ~ p

Implikasi Konvers Invers Kontraposisi

p q ~ p ~ q p  q q  p ~ p  ~ q ~ q  ~ p

T T F F T T T T

T F F T F T T F

F T T F T F F T

F F T T T T T T

Bikondisional (Bi-implikasi)

 Bentuk proposisi: “p jika dan hanya jika q”

 Notasi: p  q

p q p  q

T T T

T F F

F T F

F F T 5

Tabel kebenaran

Tabel 1.1 Tabel kebenaran konjungsi, disjungsi, dan ingkaran

p	Q	p ^ q
T	T	T
T	F	F
F	T	F
F	F	F

p	Q	p  v q
T	T	T
T	F	T

Tautologi dan Kontradiksi

 Proposisi majemuk disebut tautologi jika ia benar untuk semua kasus

 Proposisi majemuk disebut kontradiksi jika ia salah untuk semua kasus.

TAUTOLOGI

Contoh:

Lihat pada argumen berikut:

Jika Tono pergi kuliah, maka Tini juga pergi kuliah. Jika Siska tidur, maka Tini pergi kuliah. Dengan demikian, jika Tono pergi kuliah atau Siska tidur, maka Tini pergi kulah.

Diubah ke variabel proposional:

A  Tono pergi kuliah

B  Tini pergi kuliah

C  Siska tidur

Diubah lagi menjadi ekspresi logika yang terdiri dari premis-premis dan kesimpilan. Ekspresi logika 1 dan 2 adalah premis-premis, sedangkan ekspresi logika 3 adalah kesimpulan.

(1)   A → B                                    (Premis)

(2)   C → B                         (premis)

(3) (A V C) → B              (kesimpulan)

Maka sekarang dapat ditulis: ((A → B) ʌ (C → B)) → ((A V C) → B 

Dari tabel kebenaran diatas menunjukkan bahwa pernyataan majemuk :

 ((A → B) ʌ (C → B)) → ((A V C) → B adalah semua benar (Tautologi)[2].

Contoh tautologi dengan menggunakan tabel kebenaran:

 (p ʌ  ~q)  p

Pembahasan:

p	q	~q	(p ʌ ~q)	(p ʌ ~q)  p
B B S S	B S B S	S B S B	S B S S	B B B B

Ini adalah tabel kebenaran yang menunjukkan Tautologi dengan alasan yaitu semua pernyataannya bersifat benar atau True (T). maka dengan perkataan lain pernyataan majemuk (p ʌ ~q)  p selalu benar.

 [(p  q) ʌ p] p  q

Berdasrkan tabel diatas pada kolom 5, nilai kebenaran pernyataan majemuk itu adalah BBBB. Dengan perkataan lain, pernyataan majemuk           [(p  q) ʌ p] p  q selalu benar

Pembuktian dengan cara kedua yaitu dengan penjabaran atau penurunan dengan menerapkan sebagian dari 12 hukum-hukum ekuivalensi logika.

Contoh:

 (p ʌ q)  q

Penyelesaian:

(p ʌ q)  q  ~(p ʌ q) v q

~p v ~q v q

 ~p v T

 T ………….(Tautologi)

Dari pembuktian diatas telah nampaklah bahwa pernyataan majemuk dari (p ʌ q)  q adalah tautologi karena hasilnya T (true) atau benar.

Pembuktian dengan menggunakan tabel kebenaran dari pernyataan majemuk  (p ʌ q)  q

KONTRADIKSI

Contoh dari Kontradiksi:

 (A ʌ ~A)

Pembahasan:

A	~A	(A ʌ ~A)
B S	S B	S S

Dari tabel kebenaran diatas dapatlah disimpulkan bahwa pernyataan majemuk (A ʌ ~A) selalu salah.

 P ʌ (~p ʌ q)

Ekivalensi Logika

 Dua buah proposisi majemuk, P(p, q, ..) dan Q(p, q, ..) disebut ekivalen secara logika jika keduanya mempunyai tabel kebenaran yang identik.

Notasi: P(p, q, …)  Q(p, q, …)

Contoh . Hukum De Morgan: ~(p  q)  ~p  ~q.

p q p  q ~ (p  q) ~ p ~q ~ p  ~ q 

Hukum – Hukum Proposisi

Proposisi, dalam kerangka hubungan ekivalen logika, memenuhi sifat-sifat yang dinyatakan dalam sejumlah hukum pada tabel di bawah.Beberapa hukum tersebut mirip dengan hukum aljabar pada system bilangan riil, misalnya a(b + c) = ab + ac, yaitu hukum distributif, sehingga kadang-kadang hukum logika proposisi dinamakan juga hukum-hukum aljabar proposisi.

Hukum-hukum logika di atas bermanfaat untuk membuktikan ke-ekivalenan dua buah proposisi. Selain menggunakan tabel kebenaran, ke-ekivalenan dapat dibuktikan dengan hukum-hukum logika, khususnya pada proposisi majemuk yang mempunyai banyak proposisi atomik. Bila suatu proposisi majemuk mempunyai n buah proposisi atomic, maka table kebenarannya terdiri dari  baris. Untuk n yang besar jelas tidak praktis menggunakan tabel kebenaran, misalnya untuk n=10 terdapat  baris di dalam tabel kebenarannya

Implikasi

Adalah suatu pernyataan majemuk p dan q yang digabung dengan memakai kata hubung logika “jika…maka…”.

Implikasi suatu pernyataan dilambangkan dengan p→q. Dibaca :

 Jika p maka q

 p berimplikasi q

 q hanya jika p

 p syarat cukup untuk q

 q syarat perlu untuk p

Pada  implikasi, p disebut anteseden (hipotesis), q disebut konklusi (kesimpulan).

Nilai kebenaran: untuk p→q bernilai salah hanya berlaku untuk p pernyataan bernilai benar dan q pernyataan bernilai salah.

Implikasi Logis

“jika Andi rajin belajar maka Andi naik kelas”

Jika pada kenyataannya Andi rajin belajar maka sebagai konskuensi logis dari pernyataan di atas pasti Andi naik kelas.

Misal     p: Andi rajin belajar

                        q: Andi naik kelas

                                maka ((p→q)∧p)→q, nilainya akan selalu benar.

p	Q	p→q	((p→q)∧p)	((p→q)∧p)→q
B	B	B	B	B
B	S	S	S	B
S	B	B	S	B
S	S	B	S	B

FUNGSI PROPOSISI DAN HIMPUNAN KEBENARAN

Misalkan P(x) merupakan sebuah pernyataan yang mengandung variabel x dan D adalah sebuah himpunan (sembarang kumpulan obyek). Kita menyebut P sebuah fungsi proposisi (dalam D) jika untuk setiap x di D, P(x) adalah proposisi.

 

BAB 13 Definisi fungsi

 DEFINISI FUNGSI

Sebuah fungsi f adalah suatu aturan korespondensi yang menghubungkan setiap objek x dalam satu himpunan, yang disebut daerah asal, dengan sebuah nilai tunggal f(x) dari suatu himpunan kedua. Himpunan nilai yang diperoleh secara demikian disebut daerah hasil fungsi. Lihat gambar berikut :

Cara mencari daerah asal dan daerah hasil
Contoh : Carilah daerah asal dan daerah hasil dari fungsi

 

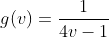Penyelesaian :
Daerah Asal untuk f adalah :

Daerah hasil adalah :
Rubah dulu fungsi diatas dengan variabel y menjadi

Membedakan fungsi satu-satu (one to one) dan Fungsi pada (onto)

Dalam suatu fungsi ada yang merupakan hanyaFungsi Pada atau Fungsi Satu-Satu saja tapi ada yang termasu kedua-duanya. Fungsi yang merupakan fungsi satu-satu dan pada biasanya disebut dengan Fungsi Bijeksi. 

Satu-Satu dan Fungsi Pada.

Secara sederhana bahwa Fungsi Bijeksi akan terjadi jika jumlah anggota domain sama dengan jumlah anggota kodomain. Dengan catatan bahwa tidak ada dua domain berbeda atau lebih dipetakan ke kodomain yang sama dan setiap kodomain memiliki pasangan di domain.

Keterangan :

Pemetaan pertama merupakan Fungsi Bijeksi karena sudah sesuai dengan Difinisi.

Pemetaan kedua bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi Pada. Perhatikan “d” dan “e” di domain, kedua anggota domain tersebut dipetakan ke anggota domain yang sama

Pemetaan ketiga bukan Fungsi Bijeksi karena pada pemetaan tersebut hanya terjadi Fungsi Satu-Satu. Karena terdapat anggota kodomain yaitu “9″ yang tidak memiliki pasangan pada anggota domain.

FUNGSI SATU KE SATU (ONE TO ONE)

Fungsi di atas, fungsi dikatakan satu-ke-satu (one-to-one) atau injektif (injective) jika tidak ada dua elemen himpunan A yang memiliki bayangan sama.

Contoh. Relasi adalah fungsi satu-ke-satu,
Tetapi relasi ke bukan fungsi satu-ke-satu,

FUNGSI PADA atau (ONTO)

Fungsi f dikatakan dipetakan pada (onto) atau surjektif (surjective) jika setiap elemen himpunan B merupakan bayangan dari satu atau lebih elemen himpunan A.

Dengan kata lain seluruh elemen B merupakan jelajah dari f. Fungsi f disebut fungsi pada himpunan B. 

Membedakan domain, kodomain dan range suatu fungsi

Pengertian Domain, Kodomain, Range Domain disebut juga dengan daerah asal,

 kodomain daerah kawan, sedangkan range adalah daerah hasil.

contoh : Diketahui himpunan P = { 1,2,3,4 } dan himpunan Q = { 2,4,6,8,10,12 }

Relasi dari himpunan P ke himpunan Q dinyatakan dengan " setengah dari ".

Jika relasi tersebut dinyatakan dengan himpunan pasangan berurutan menjadi :

{ (1,2),(2,4),(3,6),(4,8) }.

Relasi di atas merupakan suatu fungsi karena setiap anggota himpunan P mempunyai tepat satu kawan anggota himpunan Q.

Dari fungsi di atas maka :

Domain/daerah asal = himpunan P = { 1,2,3,4 }

Kodomain/daerah kawan = himpunan Q = { 2,4,6,8,10,12 }

Range/daerah hasil = { 2,4,6,8 }

Jika A = {2, 3, 6} B = {2, 4, 6, 8, 10, 11}. Relasi dari himpunan A ke B adalah “

Faktor dari “, nyatakanlah relasi tersebut dengan :

a. Diagram Panah

b. Diagram Cartesius

c. Himpunan pasangan berurutan.

sehingga diperoleh daerah hasilnya adalah :

BAB 12 RELASI

A.Pengertian Relasi

Suatu relasi (biner) F dari himpunan A ke himpunan B adalah suatu perkawanan elemen-elemen di A dengan elemen-elemen di B. didefinisikan sebagai berikut :
Definisi: Suatu fungsi f dari himpunan A ke himpunan B adalah suatu relasi yang memasangkan setiap elemen dari A secara tunggal, dengan elemen pada B.

B.Sifat Fungsi

Dengan memperhatikan bagaimana elemen-elemen pada masing-masing himpunan A dan B yang direlasikan dalam suatu fungsi, maka kita mengenal tiga sifat fungsi yakni sebagai berikut :
1. Injektif (Satu-satu)Misalkan fungsi f menyatakan A ke B maka fungsi f disebut suatu fungsi satu-satu
(injektif), apabila setiap dua elemen yang berlainan di A akan dipetakan pada dua elemen yang berbeda di B. Selanjutnya secara singkat dapat dikatakan bahwa f:A→B adalah fungsi injektif apabila a ≠ a’ berakibat f(a) ≠ f(a’) atau ekuivalen, jika f(a) = f(a’)
maka akibatnya a = a’.
2. Surjektif (Onto)
Misalkan f adalah suatu fungsi yang memetakan A ke B maka daerah hasil f(A) dari fungsi f adalah himpunan bagian dari B. Apabila f(A) = B, yang berarti setiap elemen di B pasti merupakan peta dari sekurang-kurangnya satu elemen di A maka kita katakan f adalah suatu fungsi surjektif atau “f memetakan A Onto B”.
3.Bijektif (Korespondensi Satu-satu)
Suatu pemetaan f: A→B sedemikian rupa sehingga f merupakan fungsi yang injektif dan surjektif sekaligus, maka dikatakan “f adalah fungsi yang bijektif” atau “ A dan B berada dalam korespondensi satu-satu”

C.Jenis – jenis Fungsi

Jika suatu fungsi f mempunyai daerah asal dan daerah kawan yang sama, misalnya D, maka sering dikatakan fungsi f pada D. Jika daerah asal dari fungsi tidak dinyatakan maka yang dimaksud adalah himpunan semua bilangan real (R). Untuk fungsi-fungsi pada R kita kenal beberapa fungsi antara lain sebagai berikut.
a. Fungsi Konstan
b. Fungsi Identitas
c. Fungsi Linear
d. Fungsi Kuadrat
e. Fungsi Rasional
artikel diatas hanya pengertian singkat dari relasi, fungsi dan jenis fungsi,untuk artikel lengkapnya tentang artikel diatas silakan download artikel ini dalam format PDF dibawah ini…

D. Cara Menyatakan Relasi

Relasi dari dua himpunan A dan himpunan B dapat dinyatakan dengan 3 cara yaitu diagram panah, diagram Cartesius, dan Himpunan pasangan berurutan. Untuk penjelasan ketiga cara ini adalah sebagai berikut:
Diagram panah

Cara membuat relasi dengan diagram panah adalah

Himpunan pertama atau himpunan A diletakkan di sebelah kiri
Himpunan kedua atau himpunan B diletakkan di sebelah kanan
Buatlah anak panah menunjukkan relasi antara himpunan A dengan himpunan B.

Contoh:

Cara membuat relasi dengan diagram Cartesius adalah

Anggota himpunan pertama atau himpunan A diletakkan pada sumbu horizontal
Anggota himpunan kedua atau himpunan B diletakkan pada sumbu vertikal
Buatlah Noktah (∙) yang menunjukkan relasi antara himpunan A dengan himpunan B.

Misalnya
Himpunan Pasangan Berurutan

Relasi dari himpunan A ke himpunan B dapat dinyatakan dengan (x, y) jika x ∈ A dan y ∈ B

Cara menyatakan relasi dengan himpunan pasangan berurutan adalah

Pasangan diletakkan di dalam kurung dan dipisahkan oleh koma.
Anggota himpunan pertama atau himpunan A diletakkan pada bagian depan
Anggota himpunan kedua atau himpunan B diletakkan di belakang

Misalnya: Nyatakan himpunan berikut dalam himpunan pasangan berurutan dengan relasi “kurang dari”

Jika A = {1, 2, 3, 4}

B = {1, 2, 3, 4, 5}

Penyelesaian

1 kurang dari 2, 3, 4, 5

2 kurang dari 3, 4, 5

3 kurang dari 4,5

4 kurang dari 5

maka himpunan pasangan berurutnya adalah:

{(1, 2), (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5), (3, 4), (3, 5), (4, 5)}

BAB 10 Himpunan Dan Bilangan

A.      PENGERTIAN HIMPUNAN

Himpunan merupakan kumpulan benda-benda atau objek-objek yang telah terdefinisi secara jelas  atau sekumpulan objek yang mempunyai satu kesatuan serta mempunyai keterikatan diantara anggota-anggotanya.

Contoh himpunan:

-          Kumpulan kata dalam kamus

-          Kumpulan buku dalam perpustakaan

Sifat keterikatan yang ada dalam kumpulan tersebut biasa disebut sifat-sifat dari himpunan:

1.       Setiap objek dapat dibedakan dari yang satu dengan yang lainnya yang ada dalam unsur/elemen dari himpunan itu sendiri.

2.       Dapat dibedakan mana anggota himpunan dan mana yang bukan.

B.      MENYATAKAN ATAU MENULIS  SUATU HIMPUNAN

1.       Cara pendaftaran

Suatu cara yang dipergunakan untuk menulis himpunan dengan cara mendaftarkan setiap elemen / unsur dari himpunan tersebut.

Contoh : - himpunan bilangan bulat yang kurang dari sama dengan 18,

ditulis B= {0,1,2,3,...}

 -himpunan binatang berkaki 4, ditulis B= {sapi,babi,anjing,...}

2.       Cara pencirian

Suatu cara yang dipakai untuk menyatakan / menulis himpuna dengan cara menulis karakteristik dari setiap elemen / unsur himpunan tersebut.

Contoh: - himpunan bilangan real  yang 2,005<x≤10,11

                        Dinyatakan dalam bentuk pencirian menjadi  R={x/2,005<x≤10,11;xϵR}

 -himpunan bilangan bulat, dinyatakan dalam bentuk pencirian menjadi: B={x/xϵb}

C.      JUMLAH UNSUR SUATU HIMPUNAN

                Banyaknya elemen atau unsur yang terkandung didalam himpunan itu sendiri , biasanya di beri simbol “ N(A)”= kardinal.

                Contoh :

1.       A= {a,i,u,é,o,e}

“N(A)”= 6

2.       B= {-2,-1,0,1,2,3,4}

“N(A)”=7

D.      MACAM-MACAM HIMPUNAN

1.       Himpunan Kosong

2.       Himpunan Bagian

3.       Himpunan Bagian Sejati

Jika A adalah suatu himpunan dan B juga merupakan suatu himpunan maka himpunan A dikatakan himpunan bagian yang sejati dari himpunan B , jika dan hanya jika untuk setiap x elemen berada dalam himpunan B , paling sedikit sekurang kurangnyaada 1 elemen B Yang tidak berada dalam himpunan A.

Contoh :

1.       A= {1,3,5,7}

B=Himpunan bilangan bulat positif yang kurang dari 25

Jadi ACB adalah himpunan bagian sejati

4.    Himpunan berhingga

Suatu himpunan yang elemen unsur/ anggotanya dapat dihitung banyaknya atau berhingga  banyaknya. Biasanya untuk menyatakan atau menulis himpunan ini tidak perlu ditulis secara keseluruhan dari elemen-elemennya ,cukup ditulis anggota awalnya serta anggota akhirnya.

Contoh :

1.       A=himpunan bilangan bulat positif < 2000

Jadi A={0,1,2,3,4,...,1999}

5.    Himpunan Tak Berhingga

Suatu himpunan yang elemen / unsur maupun anggotanya tidak dapat dihitung banyaknya(tak berhingga). Untuk menyatakan / menulis himpunan ini tidak perlu ditulis semuanya ukup ditulis elemen awal  dan titulis 3 titik tanpa ada elemen berikutnya.

Contoh:

1.       Himpunan bilangan asli

Jadi A= {1,2,3,...}

2.       Himpunan bilangan bulat

Jadi B={...,-2,-1,0,1,2,3,...}

6.    Himpunan Semesta(S)

Suatu himpunan yang elemen/unsur anggotanya merupakan keseluruhan dari objek objek pembicaraan didalam himpunan itu sendiri.

Contoh :

1.       A= himpunan garis yang saling berpotongan dalam suatu bidang datar

B= Himpunan suatu kurva yang saling berpotongan dalam suatu bidang datar

Jadi himpunan semesta adalah kumpulan titik-titik pada suatu bidang datar

7.    Himpunan Complument ( Ac)

Jika S adalah himpunan semesta dan A merupakan suatu himpunan bagian dari himpunan S, Maka Ac adalah suatu himpunan yang elemen atau unsur atau anggotanya adalah yang tidak berada pada himpunan A itu sendiri.

8.    Himpunan Bersandi

Jika A dalah himpunan dan B juga himpunan maka Himpunan A dikatakan himpunan bersandi  dari himpunan B jika dan hanya jika paling sedikitnya ada satu atau lebih unsur atau elemen dari kedua himpunan tersebut mempunyai anggota yang sama.

Contoh ;

1.       A= {1,2,3,4,5,6,7,8,9,10}

B= {5,7,9,11,13,15,17}

Jadi A bersandi B= {5,7,9}

9.    Himpunan Lepas

Jika A adalah suatu Himpunan dan B juga himpunan , maka A dikatakan himpunan lepas dari himpunan b jika dan hanya jiak kedua himpunan tersebut tidak mengandung unsur atau elemen yang saling bersekutu.

Contoh:

1.       A = {x/x bilangan ganjil}

B = {x/x bilangan genap}

Jadi A himpunan lepas B

10. Himpunan Sama

Jika A suatu himpunan dan b juga merupakan suatu himpunan maka himpunan A dikatakan Himpunan sama dengan himpunan B ,jika dan hanya jika untuk setiap x elemen berada dalam himpunan A dan x elemen berada pula pada himpunan B , begitu pula sebaliknya, maka dikatakan himpunan sama.

Contoh :

1.       A={a,i,u,e,o}

B={u,e,o,a,i}

Jadi A=B

2.       C={0,1,2,3,4,5,6}

D= {Himpunan Bilangan bulat positif yang kurang dariu dan sama dengan 6}

Jadi C=D

11. Himpunan Sederajat

Jika A merupakan suatu himpunan dan b juga merupaakan suatu himpunan, maka himpunan a dikatakan himpunan sederajat dengan himpunan B jika dan hanya jika kedua himpunan tersebut mempunyai jumlah bilangan kardinal.

Contoh ;

1.       A={a,b,c,d,e,f,g}

B={0,1,2,3,4,5,6}

N(A)= 7

N(B)=7

N(A)=N(B)

Jadi A sederajat dengan B

E. KAIDAH PENULISAN DAN NOTASI HIMPUNAN

Subjek	Notasi
Nama himpunan	Huruf Besar
Elemen himpunan	Huruf kecil
Jenis Bilangan Bilangan Asli  Bilangan Bulat  Bilangan Riil  Bilangan Rasional  Bilangan Kompleks	Macam notasi N Z R R C
Himpunan kosong	atau
Operasi gabungan dua himpunan
Operasi irisan dua himpunan
Subhimpunan, Subhimpunan sejati, Superhimpunan, Superhimpunan sejati	, , ,
Komplemen
Himpunan kuasa
Semesta pembicaraan
Penulisan himpunan menggunakan tanda kurung kurawa dan dipisahkan oleh tanda koma	{ x, y,}
Himpunan yang anggotanya tidak terhingga dinyatakan dengan 3 titik	{A, B, C, …}
Keanggotaan himpunan dinyataan dengan	∈
Jumlah anggota suatu himpunan dinyatakan dengan n.	A= {1,2, 3, 4…}

 

F. CARA MENYATAKAN SUATU HIMPUNAN.

Untuk menyatakan suatu himpunan dapat menggunakan cara berikut, yaitu:

1. Cara menyatakan himpunan dengan kata-kata

Suatu himpunan dapat dinyatakan dalam bentuk kalimat dengan menuliskan syarat-syarat keanggotaan. Contoh cara menyatakan himpunan dalam bentuk kalimat antara lain adalah:

• Himpunan bilangan asli yang kurang dari tujuh
• Himpunan siswa kelas 3 yang berambut ikal
• Himpunan bilangan bulat yangkurang dari 10 dan habis di bagi 2

2. Cara menyatakan himpunan dengan notasi pembentuk himpunan

Menyatakan himpunan dengan cara ini digunakan untuk menyatakan himpunan yang anggotanya tidak terhingga. Secara umum bentuk notasi himpunan adalah sebagai berikut:

{X| . . .,X ∈ . . .}

Contohnya: A = {X|X < 10, X ∈ A}

3. Cara menyatakan himpunan dengan mendaftar

Menyatakan himpunan dengan mendaftar adalah suatu cara menyatakan himpunan dengan cara mendaftar dan memilik anggota himpunan bilangan tersebut satu per satu. Contoh cara menyatakan himpunan  dengan mendaftar:

• D adalah bilangan genap kurang dari 7, maka D = {2,4,6}
• F adalah bilangan prima kurang dari 10, maka F = {1, 3, 5, 7}

Untuk mempelajari artikel tentang himpunan secara lebih detail lagi silah membuka halaman kamus Q yang berlabel Himpunan.

MACAM-MACAM BILANGAN

1. BILANGAN RIIL (BILANGAN NYATA)

2. BILANGAN RASIONAL

3. BILANGAN IRRASIONAL

4. BILANGAN BULAT

5. BILANGAN ASLI

6. BILANGAN PRIMA

7. BILAGAN CACAH

8. BILANGAN IMAJINER (BILANGAN KHAYAL)

9. BILANGAN KOMPLEKS

10. BILANGAN KOMPOSIT